動点問題について書きます
考え方の進め方が
教科書通りにやると
面倒
間違えやすい
時間がかかる
分かりにくい
のでそこらへんを
問題
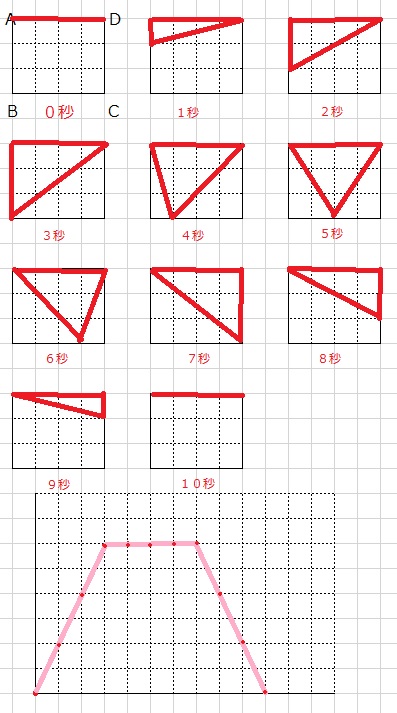
AB=3㎝
BC=4㎝の長方形があります
点Pが
秒速1㎝の速さで
A→B→C→D
と移動します
その時の
△APDの面積を調べる問題です
xが時間、yが△APDの面積を表します
書き出す
まず
△APDを1秒毎にかいていきます
面倒ですが
これをすることが理解へとつながります
書いて、面積を求めていきます
グラフに起こす
ここがポイントで
教科書と
教科書準拠の問題集では
ここで
「xとyの関係を表す式を求める」
という問題が出てきます
しかし
書き出した図から
式を求めるのは難しいのです
なので
まず、グラフに起こします
対応する座標に点を打ち、つなげていきます
関係式を求める
グラフをかいてから
関係を表す式を求めていきます
今回例に出した問題なら
上に上がっていく部分
傾きが2で切片0なので
y=2x(0≦x≦3)
グラフから定義域もすぐわかります
横線の部分は
y=6(3≦x≦7)
下に下がっていく部分は
傾きはー2
切片はbと置いて計算で求めていけばいいでしょう
(10,0)を通るから
0=-2×10+bより
b=20
よって
y=-2x+20(7≦x≦10)
となります
視覚化すると分かりやすい
頭で考えるより
目で見えるようにしてから考える
これは
この問題だけでなく
数学の問題の多くに当てはまります
図や表を書く手間を
面倒くさがらず
書いていきましょう
 ブログ|愛知・小牧市で論理力を高める算数・数学の塾|遊学塾 |
ブログ|愛知・小牧市で論理力を高める算数・数学の塾|遊学塾 |