見直しってどうやるの？

テストを一通りやったら

「見直しするんだよ」

って言われるけど、やっても間違えちゃうんだけど…

という声の上がる

「見直し」

についてちょっと書いてみましょう。

ただし、これは、こういうやり方もあるよ的ものであるので、そういう目でご覧ください。

２０１９年度愛知県公立入試A日程でお試し

見直す科目と言えば
「数学」
なので
数学の大問１に絞って、書いていきます。
野田塾さんのところのをリンクしました。

大問1(1)

　８－（－３）
＝８＋３
＝１１
と解きます。
では、見直します。
８－（２－５）＝ｘ
と置きます。
８＝ｘ＋（２－５）
と移項します。
８＝ｘ＋（－３）
８＝ｘ－３
ここで、普通に計算した「１１」をｘに代入します。
両辺が等しくなりました。
これで、「まずは」正解だろうと安心できます。

（２）

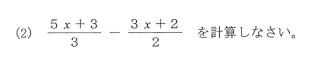
正解は
「６分の１ｘ」です。
見直ししていきましょう。
与式のXに１を代入していきます。
（５+３）/3－（3+2）/2
＝8/3-5/2
＝16/6-15/6
＝1/6
答えの、ｘに１を代入すると、
１/6になりました。
これで、「ほぼ」正解と言えますね。

（３）

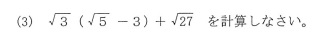
√２７はさすがにそのままとは言えず
３√３に変形してください。
これができないレベルでは、もともと公立は難しいですしね。
さて、
答えは
「√１５」です。
では、見直しです。
√３をｘ、√５をｙとします。
　ｘ（ｙ－３）＋３ｘ
＝ｘｙ－３ｘ＋３ｘ
＝ｘｙ
となったので、ｘ、ｙを数値に戻します。
√３×√５＝√１５
同じになりました。

（４）

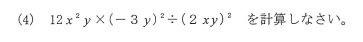
正解は「２７ｙ」
では、見直していきましょう。
ｘ＝１、ｙ＝２を代入します。
１２×１×２×（－３×２）＾２÷（２×１×２）＾２
（＾２は２乗を表しています）
　２４×（－６）＾２÷４＾２
＝２４×３６÷１６
＝５４
答えに、ｙ＝２を代入すると、５４になりました。
ほぼ正解ですね。一安心できます。

（５）

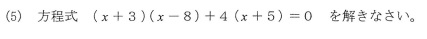
答えは、（１±√１７）/2
と厄介です。
さて、どう見直しましょうか？
答えのうちの大きい方
（１＋√１７）/2に注目します。
これよりちょっと小さい数は
（１＋√９）/２
ちょっと大きい数は
（１＋√２５）/2
です。
それぞれ計算すると
２と３になります
これを
基の式に代入すると
（２+３）（２－８）＋４（２＋５）
＝５×（－６）＋４×７
＝－３０＋２８
＝－２
大きい方は
（３＋３）（３－８）＋４（３＋５）
＝６×（－５）＋４×８
＝－３０＋３２
＝２
ｘ＾２が正ならば
２つの解のうち、大きい方は
近似値の小さい方は、答えが負
近似値の大きい方は、答えが正
になります。
詳しいことは、高校に入った後の「二次関数」の単元で勉強することですが、
ここでは、無理やりですが使いました。

まとめ

見直しのときに大事なことは
「解いた方法とは
違う方法
で考える」
という点です。
同じ方法で解きなおしていると、
同じところで間違えてしまう確率が上がってしまいます。
Aの方法で解いたら、Bの方法で確認
です。